Ozaner Hansha

\(\displaystyle{\LARGE{\text {Oz}}\mkern-1mu{\tiny\underbrace{\LARGE {\text {∀n∈ℝ}}}_{\small {\text {For all real n...}}}}}\)

My notes on math, computer science, philosophy, personal projects, and more.

Combinations

A $k$-combination of a set $S$ is a set $A$ such that:

\[A\subseteq S,\,\,\,|A|=k\]

As we can see, combinations themselves aren’t all too interesting. Instead it is the enumeration of all combinations of a set that is of interest, as we’ll see below.

Binomial Coefficient

The number of $k$-combinations of a set $S$ with $n$ elements is given by the binomial coefficient:

\[\binom{n}{k}=|\{A\subseteq S: |A|=k\}|=\frac{n^{\underline {k}}}{k!}=\underbrace{\frac{n!}{k!(n-k)!}}_{\text{only if } 0\le k\le n}\]

Note this definition implies that $n<k\implies\binom{n}{k}=0$. Also note the special case $\binom{0}{0}=1$, since $\emptyset$ has exactly one subset: itself.

Proof Note that the number of ways we can pick $k$ elements from $n$ is given by principle of counting, resulting in the following falling factorial: $$n(n-1)(n-2)\cdots(n-k)=n^{\underline {k}}$$ However, this count includes all $k!$ permutations of each possible choice of $k$ elements. So, to get the count of distinct sets of $k$ elements, we simply divide by $k!$: $$\binom{n}{k}=\frac{n^{\underline {k}}}{k!}$$ Further, recalling the identity $n^{\underline {k}}=\frac{n!}{(n-k)!}$ and stipulating that $0\le k\le n$, as the factorial is not defined for negative integers, we have: $$\frac{n^{\underline {k}}}{k!}=\frac{n!}{k!(n-k)!}$$

With the binary function $\binom{n}{k}$ being read as “$n$ choose $k$”. Complementary to the notation for partial permutations, the binomial coefficient is also denoted $_nC_k$ and nCr(n,k).

The binomial coefficient has combinatorial significance in that it gives the number of ways to choose $k$ elements from a group of $n$ where order doesn’t matter.

Binomial Theorem

This eponymous theorem tells us that the expansion of a binomial raised to a power $n\in\mathbb N$ is given by:

\[(x+y)^n=\sum_{k=0}^n\binom{n}{k}x^{n-k}y^k\]

While powerful, we’ll see below that this theorem can be generalized to arbitrary polynomials.

Identities

The binomial coefficient has associated with it a mountain of identities, theorems, and equalities. Listing them all here would be superfluous, but we’ll prove two popular ones:

Sum of all Binomial Coefficients The sum of all binomial coefficients for a given $n$ is given by: $$\sum_{k=0}^n\binom{n}{k}=2^n$$ We can prove this directly via binomial theorem: $$\begin{align*} 2^n&=(1+1)^n\\ &=\sum_{k=0}^n\binom{n}{k}1^{n-k}1^k\\ &=\sum_{k=0}^n\binom{n}{k} \end{align*}$$ This identity becomes even clearer when we recall that $\binom{n}{k}$ gives the number of $k$ sized subsets of a set $S$ with $n$ elements. And so summing the number of subsets from $0$ to $n$ gives us the number of all subsets of an $n$ element set, or the size of its power set: $$|\mathcal{P}(S)|=2^n$$
Pascal's Rule Pascal's rule is the following recurrence relation: $$\binom{n-1}{k}+\binom{n-1}{k-1}=\binom{n}{k}$$ We can prove this via the following chain of equalities: $$\begin{align*} \binom{n-1}{k}+\binom{n-1}{k-1}&=\frac{(n-1)!}{k!(n-k-1)!}+\frac{(n-1)!}{(k-1)!(n-1-k+1)!}&\text{(def. of binomial coefficient)}\\ &=(n-1)!\left(\frac{1}{k!(n-k-1)!}+\frac{1}{(k-1)!(n-k)!}\right)&\text{(algebra)}\\ &=(n-1)!\left(\frac{n-k}{k!(n-k)!}+\frac{k}{k!(n-k)!}\right)&\text{($(n+1)!=(n+1)\cdot n!$)}\\ &=(n-1)!\left(\frac{n}{k!(n-k)!}\right)&\text{(algebra)}\\ &=\frac{n!}{k!(n-k)!}=\binom{n}{k}&\text{(def. of binomial coefficient)} \end{align*}$$ Note an alternate form of this identity is given by increasing both $n$ and $k$ by $1$: $$\binom{n}{k+1}+\binom{n}{k}=\binom{n+1}{k+1}$$ As we'll see in the next section, this identity provides the basis for a particularly interesting visualization of the binomial coefficient.

Infinite Cardinals

Up until now, we’ve only been counting combinations of finite sets. Despite this, however, the definition of the binomial coefficient generalizes to infinite cardinals as well. For a set $A$ with cardinality $\alpha$ and a cardinal $\beta$:

\[\binom{\alpha}{\beta}=|\{B\subseteq A:|B|=\beta\}|= \begin{cases} \alpha^\beta, & \beta\le\tiny\underbrace{\normalsize\alpha}_ {\small\text{infinite}}\normalsize\\ \frac{\alpha^{\underline\beta}}{\beta!}, & \beta\le\tiny\underbrace{\normalsize\alpha}_ {\small\text{finite}}\normalsize\\ 0, & \beta>\alpha \end{cases}\]

There are 2 special cases of this definition not seen in the finite case:

  • if $\alpha$ is infinite and $\beta$ is finite, we have $\binom{\alpha}{\beta}=\alpha^\beta=\alpha$
  • if $\alpha=\beta$ and are infinite, we have $\binom{\alpha}{\beta}=\alpha^\beta=2^\alpha=2^\beta$

Pascal’s Triangle

Pascal’s triangle is a visual representation of the binomial coefficients that not only serves as an easy to construct lookup table, but also as a visualization of a variety of identities relating to the binomial coefficient:

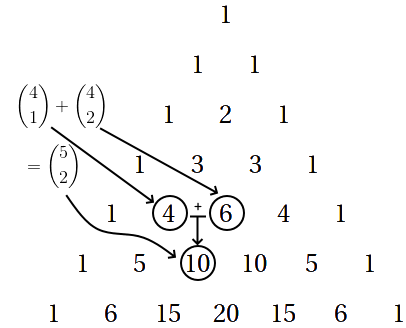
pascal

Each row and column is represented by a natural number starting from $0$. The number in row $n$ and column $k$ is given by $\binom{n}{k}$.

While the staggering of the columns may make this unclear, the $k$th element from the left of row $n$ is said to be in column $k$.

As we can see, by starting with just the first two rows we can iteratively construct Pascal’s triangle using Pascal’s rule (which we proved earlier).

We can generalize Pascal’s triangle to a pyramid and, more generally, an $n$ dimensional simplex via the multinomial version of Pascal’s rule discussed further below.

Multinomial Coefficient

Recall that the binomial coefficient gives us the number of ways to pick $k$ items from a group of $n$, leaving $n-k$ items left over. As such, we could also interpret this as being the number of ways to split a group of $n$ into two groups of size $k$ and $n-k$ respectively.

The multinomial coefficient generalizes this combinatorial problem, giving the number of ways to split a group of $n$ into $r$ groups of sizes $k_1,k_2,\cdots,k_r$ where $\sum_{i=0}^r k_i=n$. It is denoted and given by the following:

\[\binom{n}{k_1,k_2,\cdots,k_r}=\frac{n!}{k_1!k_2!\cdots k_r!}\]
Proof We have $n$ choose $k_1$ combinations for the first group, $n-k_1$ choose $k_2$ for the second, and so on. The principle of counting tells us then that the number is: $$\binom{n}{k_1}\binom{n-k_1}{k_2}\cdots\binom{n-k_1-k_2-\cdots k_{r-1}}{k_r}$$ This gives us a sort of telescoping product where we can cancel out the previous denominator with the next numerator leaving us with: $\require{cancel}$ $$\frac{n!}{k_1!\cancel{(n-k_1)!}}\frac{\cancel{(n-k_1)!}}{k_2!\cancel{(n-k_1-k_2)!}}\cdots\frac{\cancel{(n-k_1-\cdots-k_{r-1})!}}{0!k_r!}=\frac{n!}{k_1!k_2!\cdots k_r!}$$

It’s easy to see that the binomial coefficient is just a special case of the multinomial coefficient:

\[\binom{n}{k}=\frac{n!}{k!(n-k)!}=\binom{n}{k,n-k}\]

The multinomial coefficient can also be interpreted as the number permutations of a multiset, where each element $x_i$ has multiplicity $k_i$.

Multinomial Theorem

This generalization of the binomial theorem allows us to expand any multinomial raised to some nonnegative integer power $n$ in the following manner:

\[(x_1+x_2+\cdots+x_r)^n=\sum_{k_1+k_2+\cdots k_r=n}\binom{n}{k_1,k_2,\cdots, k_r}x_1^{k_1}x_2^{k_2}\cdots x_r^{k_r}\]

Where the sum is over all tuples $(k_1,k_2,\cdots,k_r)\in\mathbb{N}^r$ whose elements sum to $n$.

Identities

Below we state and prove the same two identities we proved earlier but generalized for the multinomial coefficient.

Sum of all Multinomial Coefficients The sum of all multinomial coefficients with $r$ terms for a given $n$ is: $$\sum_{k_1+k_2+\cdots k_r=n}\binom{n}{k_1,k_2,\cdots,k_r}=r^n$$ Analogous to the binomial case, we can prove this directly via multinomial theorem: $$\begin{align*} r^n&=(1+1+\cdots+1)^n\\ &=\sum_{k_1+k_2+\cdots k_r=n}\binom{n}{k_1,k_2,\cdots, k_r}1^{k_1}1^{k_2}\cdots 1^{k_r}\\ &=\sum_{k_1+k_2+\cdots k_r=n}\binom{n}{k_1,k_2,\cdots, k_r} \end{align*}$$
Multinomial Pascal's Rule $$\begin{gather*} \binom{n-1}{k_1-1,k_2,\cdots,k_r}+\binom{n-1}{k_1,k_2-1,\cdots,k_r}+\cdots+\binom{n-1}{k_1,k_2,\cdots,k_r-1} \\=\binom{n}{k_1,k_2,\cdots,k_r} \end{gather*}$$ We prove this in a similar way as the binomial case: $$\begin{align*} &\phantom{=}\binom{n-1}{k_1-1,k_2,\cdots,k_r}+\binom{n-1}{k_1,k_2-1,\cdots,k_r}+\cdots+\binom{n-1}{k_1,k_2,\cdots,k_r-1}\\ &=\frac{(n-1)!}{(k_1-1)!k_2!\cdots k_r!}+\frac{(n-1)!}{k_1!(k_2-1)!\cdots k_r!}+\cdots+\frac{(n-1)!}{k_1!k_2!\cdots (k_r-1)!}\\ &=(n-1)!\left(\frac{1}{(k_1-1)!k_2!\cdots k_r!}+\frac{1}{k_1!(k_2-1)!\cdots k_r!}+\cdots+\frac{1}{k_1!k_2!\cdots (k_r-1)!}\right)\\ &=(n-1)!\left(\frac{k_1}{k_1!k_2!\cdots k_r!}+\frac{k_2}{k_1!k_2!\cdots k_r!}+\cdots+\frac{k_r}{k_1!k_2!\cdots k_r!}\right)\\ &=(n-1)!\left(\frac{k_1+k_2+\cdots+k_r}{k_1!k_2!\cdots k_r!}\right)=(n-1)!\left(\frac{n}{k_1!k_2!\cdots k_r!}\right)\\ &=\frac{n!}{k_1!k_2!\cdots k_r!}=\binom{n}{k_1,k_2,\cdots,k_r} \end{align*}$$ Using the multinomial coefficient and the recurrence relation above, we can create Pascal's pyramid for trinomials or, more generally, Pascal's simplex for some arbitrary number of dimensions.

Multiset Coefficient

A $k$-multicombination of a set $S$ is a multiset $A$ such that1:

\[A\subseteq S,\,\,\,|A|=k\]

The number of possible $k$-multicombinations of a set with $n$ elements is given by the multiset coefficient:

\[\left(\!\!{n \choose k}\!\!\right)=\binom{n+k-1}{k}=\frac{n^{\overline {k}}}{k!}=\underbrace{\frac{(n+k-1)!}{k!(n-1)!}}_{\text{only if } 0\le k,n}\]

Where $\left(\hskip -.2em{n \choose k}\hskip -.2em\right)$ is read “$n$ multichoose $k$”.

Note that unlike normal combinations, $n<k\mathrel{\rlap{\hskip .5em/}}\Longrightarrow\left(\hskip -.2em{n \choose k}\hskip -.2em\right)=0$ since $A$ can contain an arbitrary number of copies of any single element.

The multiset coefficient comes in handy for a variety of combinatoric problems, and we can phrase it as either:

  • The number of ways we can split a group of $k$ things into $n$ groups (with groups of $0$ being allowed).
  • The number of ways to choose $k$ elements from a group of $n$ with replacement, as opposed to without for a normal combination.

  1. Note that this notation is a little sloppy. A multiset like $A$ is usually represented as an ordered pair, and so it is not literally a subset of the set $S$ nor does it literally have set cardinality $k$. This particular abuse of notation, however, is common and so we use it anyway. ↩

You May Also Enjoy

Permutations

Notes on the definition, notation, and variants of the permutation.