The Dottie Number
The Dottie number, which I will denote as $\textbf{d}$, is the only real solution to the equation: $\cos x = x$

The above is what’s known as a transcendental equation. Equations like these usually have transcendental solutions and indeed, $\textbf{d}$ is transcendental. It’s decimal expansion1 is as follows:
\[\textbf{d}=0.7390851332151606...\]Fixed Point
$\textbf{d}$ is what’s called a fixed point of $\cos x$, because the cosine function maps $\textbf{d}$ to itself. As a result, repeatedly taking the cosine of $\textbf{d}$ returns the same result:
\[\cos \textbf{d} = \textbf{d} \implies \forall n\in\mathbb{N}\ \left(\underbrace{\cos\circ\cos\circ\cdots\circ\cos}_{n}\ \textbf{d}=\textbf{d}\right)\]While $\textbf{d}$ is the $\cos$ function’s only real fixed point, there exists infinitely many solutions to $\cos z=z$ for the complex numbers. Those solutions, however, are not attractors.
Universal Attractor
What’s interesting about $\textbf{d}$ is that it’s not just the unique real fixed point of $\cos$ but that it’s also a universal attractor over the reals. That is to say, if you take the cosine of any real number and repeatedly take the cosine of the result, the result always converges to $\textbf{d}$:
\[\forall x_0\in\mathbb{R} \left(\lim_{n\to\infty} \underbrace{\cos\circ\cos\circ\cdots\circ\cos}_{n}\ x_0=\textbf{d}\right)\]Alternatively, put in terms of a sequence $x_n$:
\[\begin{align*} x_0&\in\mathbb R\\ x_{n+1}&=\cos x_n \end{align*}\]we have the following equivalent result:
\[\lim_{n\to\infty}x_n=\textbf{d}\]Julia Set
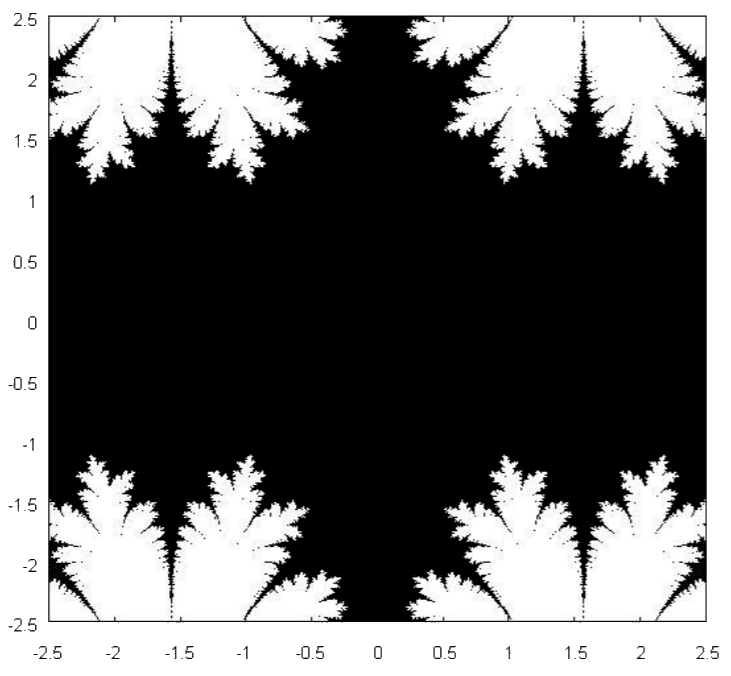
In fact, the above is true not just for $\mathbb R$ but a larger subset of $\mathbb C$ as well. We call this the fillied-in Julia set2 of $\cos$. This is the set $J_{\cos}$ of all complex numbers that converge under the aforementioned iteration, i.e.:
\[J_{\cos}=\{z_0\in\mathbb C: \left|\lim_{n\to\infty}z_n\right|<\infty\}\]As it turns out, the only number that can be converged to under this iteration is $\mathbf d$. Thus the set $J_{\cos}$ is the Dottie number’s basin of attraction, i.e. the set of all points that converge to a particular attractor.
We can visualize $J_{\cos}$ by coloring its members black on the complex plane, producing the fractal below3:
Transcendence
Yet another interesting fact about $\textbf{d}$ is that it is a transcendental number, which is to say it is not the root of a polynomial with integer coefficients. This is quite the find as there only a handful of interesting constants proven to be transcendental. Below we present a proof of $\textbf{d}$’s transcendence:
Proof
Lemma 1: LWTTo prove $\textbf{d}$'s transcendence, we'll need to make use of the Lindemann–Weierstrass theorem (LWT) which states: $$\forall x\in \mathbb{A}\left(x\not= 0\implies e^x\notin\mathbb{A} \right)$$ Or in English: $e$ to the power of any non-zero algebraic number is not algebraic (i.e. transcendental).
Lemma 2We will also wish to separately establish the following identity: $$\begin{align*} \sin^2 \textbf{d}+\cos^2 \textbf{d} &= 1&\text{(Pythagorean theorem)}\\ \sin^2 \textbf{d}+ \textbf{d}^2 &= 1&\text{($\textbf{d}$ is a fixed point)}\\ \sin \textbf{d} &= \sqrt{1-\textbf{d}^2}& \end{align*}$$
The ProofNow we can prove $\textbf{d}$'s transcendence using the LWT and Lemma 2: $$\begin{align*} e^{i\textbf{d}}&=\cos \textbf{d} + i \sin \textbf{d}&\text{(Euler's formula)}\\ &=\textbf{d}+i\sin \textbf{d} &\text{(\(\textbf{d}\) is a fixed point)}\\ &=\textbf{d}+i\sqrt{1-\textbf{d}^2} &\text{(Lemma 2)} \end{align*} $$ $$\boxed{e^{i\textbf{d}}=\textbf{d}+i\sqrt{1-\textbf{d}^2}}$$ Let us assume that $\textbf{d}$ is algebraic. If this is the case then: $$\left(\textbf{d}+i\sqrt{1-\textbf{d}^2}\right)\in \mathbb{A}$$ This is because it consists solely of algebraic numbers $\left(\textbf{d},i,1\right)$ and basic algebraic operations $\left(+,-,\times,x^2,\sqrt{x}\right)$ and thus must be root of a polynomial with rational coefficients (i.e. algebraic).
However, also assuming $\textbf{d}$ is algebraic, LWT tells us: $$e^{i\textbf{d}}\notin \mathbb{A}$$ Since the right side of the boxed equation is algebraic yet LWT guarantees that the left side is transcendental (because $i\textbf{d}$ is algebraic), we are left with a contradiction. Meaning our initial assumption, that $\textbf{d}$ is algebraic, was false. We then have the following proof by contradiction: $$\begin{align} &\textbf{d}\in\mathbb{A}\implies \left(\textbf{d}+i\sqrt{1-\textbf{d}^2}\right) \in \mathbb{A} &\text{(def. of algebraic number)}\\ &\textbf{d}\in\mathbb{A}\implies e^{i\textbf{d}}\notin \mathbb{A} &\text{(LWT)}\\ &e^{i\textbf{d}}=\textbf{d}+i\sqrt{1-\textbf{d}^2} &\text{(Euler's formula)}\\ \therefore\ &\hline{\textbf{d}\notin \mathbb{A}} &\blacksquare\\ \end{align}$$Kaplan’s Series
Kaplan4 proved that $\textbf{d}$ is equivalent to the following series:
\[\textbf{d} = \sum_{n=0}^{\infty}\ g^{\left(n\right)}\left(\frac{\pi}{2}\right)\frac{\left(-\pi\right)^n}{2^nn!}\]Where $g^{\left(n\right)}$ is the $n$th derivative of $f^{-1}$:
\[g^{\left(n\right)}\left(x\right)=\frac{d^n}{dx^n}f^{-1}\left(x\right)\]and $f^{-1}$ is the inverse of the function $f$ which is defined as:
\[f\left(x\right)=x-\cos x\]We define it in this roundabout way because there is no explicit definition of $f^{-1}\left(x\right)$, making the construction of Kaplan’s series all the more interesting.
Included below is a step by step derivation/proof of Kaplan’s series, along with how to calculate new terms manually:
Derivation and Proof
Taylor Series of $f^{-1}$To start off with, consider a function $f$ that is defined as such: $$f\left(x\right)=x-\cos x$$ Kaplan was able to construct his series by noticing a few interesting properties of this function and it's inverse $f^{-1}$ (which has no explicit definition). The first of which was it's zero: $$\begin{align} f\left(\textbf{d}\right)&=\textbf{d}-\cos \textbf{d}\\ &= \textbf{d}-\textbf{d}\\ &= 0 \end{align}$$ This implies the following about $f^{-1}$ it's inverse: $$f^{-1}\left(0\right) = \textbf{d}$$ And before we move on let's rename $f^{-1}$ to $g$ to make things less cluttered: $$f^{-1}\left(x\right) = g\left(x\right)$$ We now have an expression for $\textbf{d}$. It is simply the value of $g\left(0\right)$. We currently do not have an explicit definition of $g\left(x\right)$ but we can create one via a Taylor series: $$g\left(x\right)=\sum_{n=0}^{\infty}g^{\left(n\right)}\left(c\right)\frac{\left(x-c\right)^n}{n!}$$ Where $g^{\left(n\right)}\left(x\right)$ is the $n$th derivative of $g\left(x\right)$ and $c$ is the point we are constructing the Taylor series about. Since we are letting $n\to\infty$ the choice of constant won't affect the outcome.
Fixed point of $f$ and $g$So now let us choose a value of $c$ that will be easy to compute. Notice that: $$\begin{align} f\left(\frac{\pi}{2}\right)&=\frac{\pi}{2}-\cos \frac{\pi}{2}\\ &= \frac{\pi}{2}-0\\ &= \frac{\pi}{2} \end{align}$$ This means that $\frac{\pi}{2}$ is a fixed point of $f$ and that the following is also true of its inverse $g$: $$g\left(\frac{\pi}{2}\right)=\frac{\pi}{2}$$
$n$th derivative of $f$Also notice that finding the $n$th derivative of $f$ at $\frac{\pi}{2}$ is simple: $$\begin{align} f\left(x\right)&=x-\cos x\\ f'\left(x\right)&=1+\sin x\\ f''\left(x\right)&=\cos x\\ &\vdots\\ \left(\forall n>1\right)\ f^{(n)}\left(x\right)&=\frac{d^{n-2}}{dx^{n-2}}\cos x \end{align}$$ Because the derivatives of $\cos x$ are cyclical, we only need to evaluate the next 3 derivatives after $f''\left(\frac{\pi}{2}\right)$. Doing this we can see the pattern: $$f^{(n)}\left(\frac{\pi}{2}\right)=\{\frac{\pi}{2}, 2,0,-1,0,1,0,-1,\cdots\}$$
$n$th derivative of $g$Now knowing the $n$th derivative of $f$ at $\frac{\pi}{2}$, we can calculate the $n$th derivative of $g$ at $\frac{\pi}{2}$: $$\begin{align} f\left(g\left(x\right)\right)&=x &\text{(inverse func.)}\\ f'\left(g\left(x\right)\right)g'\left(x\right)&=1 &\text{(chain rule)}\\ g'\left(x\right)&=\frac{1}{f'\left(g\left(x\right)\right)} \end{align}$$ We can use the chain and product rules repeatedly to find the $n$th derivative of $g$. The second derivative, for example, can be computed by differentiating both sides of the above equation: $$\begin{align} f'\left(g\left(x\right)\right)g'\left(x\right)=1\\ f'(g(x))g''(x) + f''(g(x))g'(x)^2 = 0\\ f'(g(x))g''(x) = - f''(g(x))g'(x)^2\\ g''(x) = \frac{-f''(g(x))g'(x)^2}{f'(g(x))} \end{align}$$ Repeated use of the chain rule can be generalized via Faà di Bruno's formula.
Solving the Taylor Series
Using $\frac{\pi}{2}$ as our value of $c$, because $g^{(n)}(\frac{\pi}{2})$ is easy to compute, we can rewrite the Taylor series for $g$ as so:
$$g\left(x\right)=\sum_{n=0}^{\infty}g^{\left(n\right)}\left(\frac{\pi}{2}\right)\frac{\left(x-\frac{\pi}{2}\right)^n}{n!}$$
Since we are solving for $g(0)$ which equals $\textbf{d}$ we can plug it into the above series to arrive at:
$$\textbf{d}=\sum_{n=0}^{\infty}g^{\left(n\right)}\left(\frac{\pi}{2}\right)\frac{\left(-\pi\right)^n}{2^nn!}$$
Now we just have to solve for each of the terms in this sequence.
The zeroth term is equal to:
$$g\left(\frac{\pi}{2}\right)\frac{\left(-\pi\right)^0}{2^00!}=\frac{\pi}{2}$$
The first term is equal to:
$$g'\left(\frac{\pi}{2}\right)\frac{\left(-\pi\right)^1}{2^11!}=\frac{-\pi}{4}$$
Because $g'\left(\frac{\pi}{2}\right)$ can be found by plugging $\frac{\pi}{2}$ into the equation we solved earlier:
$$\begin{align}
g'\left(\frac{\pi}{2}\right)&=\frac{1}{f'\left(g\left(\frac{\pi}{2}\right)\right)}\\
&=\frac{1}{f'\left(\frac{\pi}{2}\right)}\\
&=\frac{1}{2}\\
\end{align}$$
The second term equals:
$$g''\left(\frac{\pi}{2}\right)\frac{\left(-\pi\right)^2}{2^22!}=0$$
Because $g''\left(\frac{\pi}{2}\right)$ can be found as such:
$$\begin{align}
g''(x) &= \frac{-f''(g(x))g'(x)^2}{f'(g(x))}\\
&=\frac{-f''(\frac{\pi}{2})g'(\frac{\pi}{2})^2}{f'(\frac{\pi}{2})}\\
&=-\frac{0 (\frac{1}{2})}{2}\\
&=0
\end{align}$$
Written out, the series looks something like this:
\[\textbf{d} = \frac{\pi}{4} - \frac{\pi^3}{768} - \frac{\pi^5}{61440} - \frac{43\pi^7}{165150720} - \cdots\]We can write this more succinctly, and as Kaplan originally formulated, like so:
\[\textbf{d} = \sum_{n=0}^{\infty}a_n\pi^{2n+1}\]Where $a_n$ is a sequence of rational numbers given by the above series:
| $n$ | $a_n$ |
|---|---|
| $0$ | $\frac{1}{4}$ |
| $1$ | $-\frac{1}{768}$ |
| $2$ | $-\frac{1}{61440}$ |
| $3$ | $-\frac{43}{165150720}$ |
| $4$ | $-\frac{233}{47563407360}$ |
| $\vdots$ |
The sequence $a_n$ can be found on the OEIS, with entry A302977 corresponding to the numerators and A306254 to the denominators.5
Calculating the Dottie Number
Solve Kaplan’s series
One way is to simply calculate a specified number of terms in Kaplan’s series and sum them.
\[\begin{align} \textbf{d} \approx \frac{\pi}{4} &= 0.7\color{red}{854\cdots}\\ \textbf{d} \approx \frac{\pi}{4} - \frac{\pi^3}{768} &= 0.7\color{red}{450\cdots}\\ \textbf{d} \approx \frac{\pi}{4} - \frac{\pi^3}{768} - \frac{\pi^5}{61440} &= 0.7\color{red}{400\cdots}\\ \textbf{d} \approx \frac{\pi}{4} - \frac{\pi^3}{768} - \frac{\pi^5}{61440} - \frac{43\pi^7}{165150720} &= 0.739\color{red}{2\cdots} \end{align}\]While this can provide a decent approximation, it is a very time consuming process and doesn’t allow the approximator to skip ahead to a desired accuracy (e.g. to within .01%). Moreover, while this series converges to $\textbf{d}$, it does so relatively slowly. To get just 17 decimal places of accuracy, one would need to solve for 25 terms of the series:
\[\textbf{d}\approx 0.73908 51332 15160 64\color{red}{570 711495 ...}\]General Root Finding Algorithm
Instead we might as well use a general root finding algorithm like Newton’s method or the bisection method, which allows us to calculate $\textbf{d}$ to a desired accuracy.
Analytic Solution
Since the writing of this article, a paper published by Stoutemyer has produced an analytic expression for the Dottie number:
\[\textbf{d}=\text{Inv}_1 y_0(-1)\]Where $y_0$ denotes the 0th order Spherical Bessel Function of the 2nd Kind and $\text{Inv}_1$ denotes branch 1 of it’s inverse.
-
The decimal expansion of the Dottie number is sequence A003957 in the OEIS. ↩
-
Note that, unlike the filled-in Julia Set which includes points in the interior, the Julia Set includes only the points on the boundary of the fractal. ↩
-
This image was taken from this paper by Valerii Salov. I recommend reading it if you’re interested in the Dottie number. ↩
-
While not the first to discover the constant, Samuel Kaplan was the one who named the constant after a French Professor at his university in this issue of Mathematics Magazine. This paper is also where he references the now called Kaplan series, yet doesn’t prove or elaborate on it. As a result I made this post to do just that. ↩
-
As it turns out, I was the one who added the numerator sequence into the OEIS, but it was Amiram Eldar who both added more terms to the entry as well as added the corresponding denominator sequence. ↩
