General Info

The drag force, or fluid friction, is a force that opposes the motion of an object through a fluid/gas, similar to dry friction. It can also be used to describe the resistance between a fluid in another fluid.

When the fluid is air, we refer to the force as aerodynamic drag or air resistance. When it’s water we call it hydrodynamic drag.

Non-Conservative Force

Like friction, drag is a non-conservative force, meaning the work done by it is path dependent. And also like friction, drag produces heat and thus does not conserve mechanical energy. $\renewcommand{\vec}[1]{\mathbf{#1}}$

Drag Equation

The magnitude of the drag force is given by:

\[F_D=\frac{\rho C_D A v^2}{2}\]
  • $F_D$ is the magnitude of the drag force.
  • $\rho$ is density of the fluid.
  • $C_D$ is the drag coefficient of the fluid.
  • $A$ is the cross-sectional area of the object (or more accurately the area of a projection of the object onto a plane perpendicular to the velocity).
  • $v$ is the magnitude of the velocity.

The direction of drag is opposite to that of the object’s velocity:

\[\hat{\vec{F_D}}=-\hat{\vec{v}}\]

Combining these two equations, we can write the drag force as:

\[\vec{F_D}=\frac{-\rho C_D A v^2}{2}\hat{\vec{v}}=\frac{-\rho C_D Av}{2}\vec{v}\]

Power to Overcome Drag

We can find the power required to overcome the drag force by the dot product of drag and the velocity of the object. And since the drag force is always oriented the same way as velocity, we can say:

\[P_d=\vec{F_D}\cdot\vec{v}=\frac{\rho C_DAv^3}{2}\]

Terminal Velocity

When an object is in free-fall in a liquid, gravity is counteracted by drag until it reaches an equilibrium. At this equilibrium the net force on the object, $\vec{F_{net}}$, equals zero and the object’s velocity stays constant:

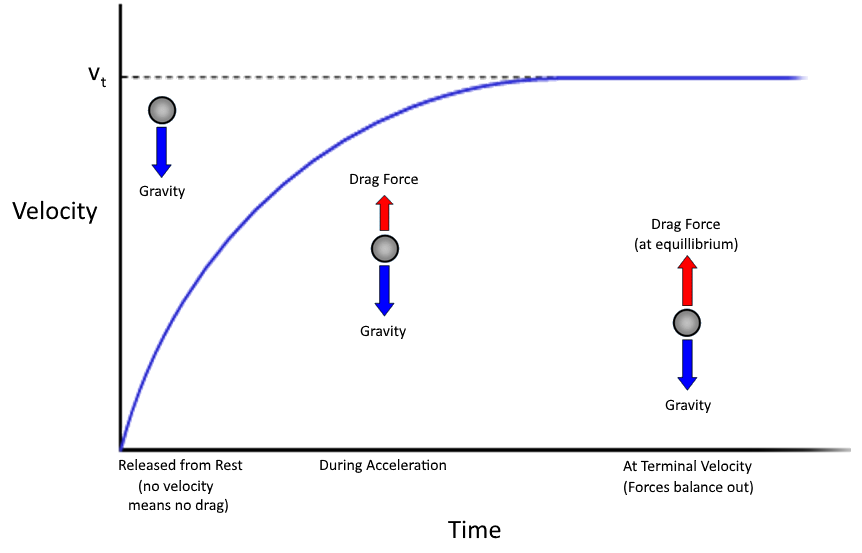
terminalvel

By solving for the velocity when the sum of the forces equals zero, we arrive at the terminal velocity $v_t$:

Derivation

$$\begin{align*} F_D-F_g&=0&\text{(when $F_D$ & $F_g$ cancel out)}\\ F_D&=F_g&\\ \frac{\rho C_DAv^2}{2}&=mg&\text{(def. of $F_D$ & $F_g$)}\\ v^2&=\frac{2mg}{\rho C_DA}& \end{align*}$$

\[\boxed{v_t=\sqrt{\frac{2mg}{\rho C_dA}}}\]

Note that this terminal velocity is more aptly described as a terminal speed, since it is just a magnitude.

Drag Coefficient

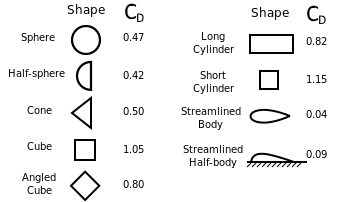
The drag coefficient is a proportionality constant used in the drag equation and is measured empirically. Objects with more blunt faces have higher drag coefficients and objects with more streamlined designs have lower ones. Here is a diagram of different drag coefficients in a particular fluid:

dragCOF